Practice 3-2 proving lines parallel – In practice 3-2, we delve into the intriguing realm of proving lines parallel, exploring the fundamental properties, theorems, and methods that empower us to establish the parallelism of lines with precision and confidence.

Parallel lines, ubiquitous in our world, exhibit a unique set of characteristics that distinguish them from other line configurations. From the parallel rails of a railway to the sides of a rectangle, these lines maintain a constant distance, never intersecting.

Understanding how to prove their parallelism is essential in various fields, including geometry, engineering, and architecture.

Parallel Line Properties

Parallel lines are two lines that never intersect, no matter how far they are extended. They have several important properties:

• The distance between parallel lines is always the same.
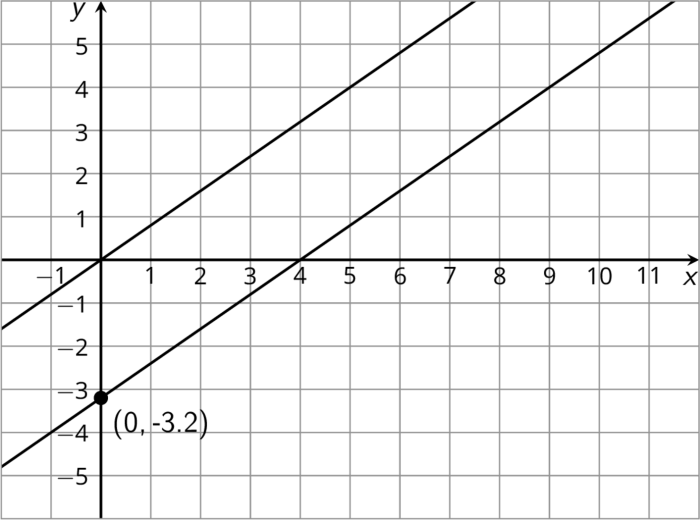
• Parallel lines have the same slope.
• If a transversal intersects two parallel lines, the alternate interior angles are congruent.
• If a transversal intersects two parallel lines, the same-side interior angles are supplementary.

Parallel lines are found in many real-life scenarios, such as the sides of a rectangle, the rails of a railroad track, or the edges of a table.

Proving Lines Parallel Using Angle Relationships

One way to prove that two lines are parallel is to use the alternate interior angles theorem. This theorem states that if a transversal intersects two parallel lines, the alternate interior angles are congruent.

To use this theorem to prove that two lines are parallel, follow these steps:

1. Draw a transversal that intersects the two lines.
2. Identify the alternate interior angles.
3. Prove that the alternate interior angles are congruent.
4. Conclude that the two lines are parallel.

Here is an example of a proof using the alternate interior angles theorem:

Given: Transversal tintersects lines land m.

Prove: l|| m

Proof:

Since tintersects land m, we have:

 ∠1 ≅ ∠3 (alternate interior angles)

 ∠2 ≅ ∠4 (alternate interior angles)

Therefore, l|| m.

Proving Lines Parallel Using Slope, Practice 3-2 proving lines parallel

Another way to prove that two lines are parallel is to use their slopes. The slope of a line is a measure of its steepness. Two lines are parallel if and only if they have the same slope.

To prove that two lines are parallel using their slopes, follow these steps:

1. Find the slope of each line.
2. Compare the slopes.
3. If the slopes are the same, the lines are parallel.
4. If the slopes are different, the lines are not parallel.

Here is an example of a proof using slopes:

Given: Line lhas a slope of 2.

Line mhas a slope of 2.

Prove: l|| m

Proof:

Since the slopes of land mare the same (2), l|| m.

Proving Lines Parallel Using Other Methods

There are other methods for proving that two lines are parallel, such as the same-side interior angles theorem and the vertical angles theorem.

The same-side interior angles theorem states that if a transversal intersects two lines, the same-side interior angles are supplementary if and only if the lines are parallel.

The vertical angles theorem states that if two lines intersect, the vertical angles are congruent.

These theorems can be used to prove that two lines are parallel in a variety of situations.

Frequently Asked Questions: Practice 3-2 Proving Lines Parallel

What is the alternate interior angles theorem?

The alternate interior angles theorem states that if two lines are cut by a transversal, the alternate interior angles are congruent.

How can I use slope to prove lines parallel?

If two lines have the same slope, they are parallel.

What is the same-side interior angles theorem?

The same-side interior angles theorem states that if two lines are cut by a transversal, the same-side interior angles are supplementary.